3.3 - La regressione logistica¶

Nella lezione precedente abbiamo introdotto l'algoritmo di regressione lineare, il cui comito è quello di "tracciare" la relazione intercorrente tra una serie di variabili indipendenti (le feature) ed una variabile dipendente che, come abbiamo visto, è continua e di tipo numerico. La regressione logistica, invece, ed a discapito del nome, è il più semplice dei classificatori, e viene usata quando abbiamo a che fare con variabili di tipo categorico.

A scopo di esempio, supponiamo di creare un modello che predica la probabilità che una mail ricevuta da un mittente a noi sconosciuto rappresenti uno spam. Indicheremo questa probabilità come \(p(mail|unknown)\).

In pratica, se il modello afferma che \(p(mail|unknown) = 0.05\), allora, in media, su \(100\) mail ricevute da indirizzi sconosciuti, \(5\) saranno di spam:

\[ \begin{align} spam &= p(mail|unknown) \cdot mail_{rec} \\ &= 0.05 * 100 \\ &= 5 \end{align} \]

Questo è un esempio di utilizzo della probabilità as is. In molti casi, tuttavia, mapperemo l'output della soluzione su un problema di classificazione binario, nel quale l'obiettivo è predire correttamente uno di due possibili label (in questo caso, spam o non spam).

La funzione sigmoidale¶

Ci si potrebbe chiedere come un modello per la regressione logistica sia in grado di asicurarsi che l'uscita ricada sempre nell'intervallo tra \(0\) ed \(1\). In tal senso, questo è assicurato dall'uso della funzione sigmoidale, definita come segue:

\[ y = \frac{1}{1+e^{-z}} \]

la cui formulazione grafica è la seguente:

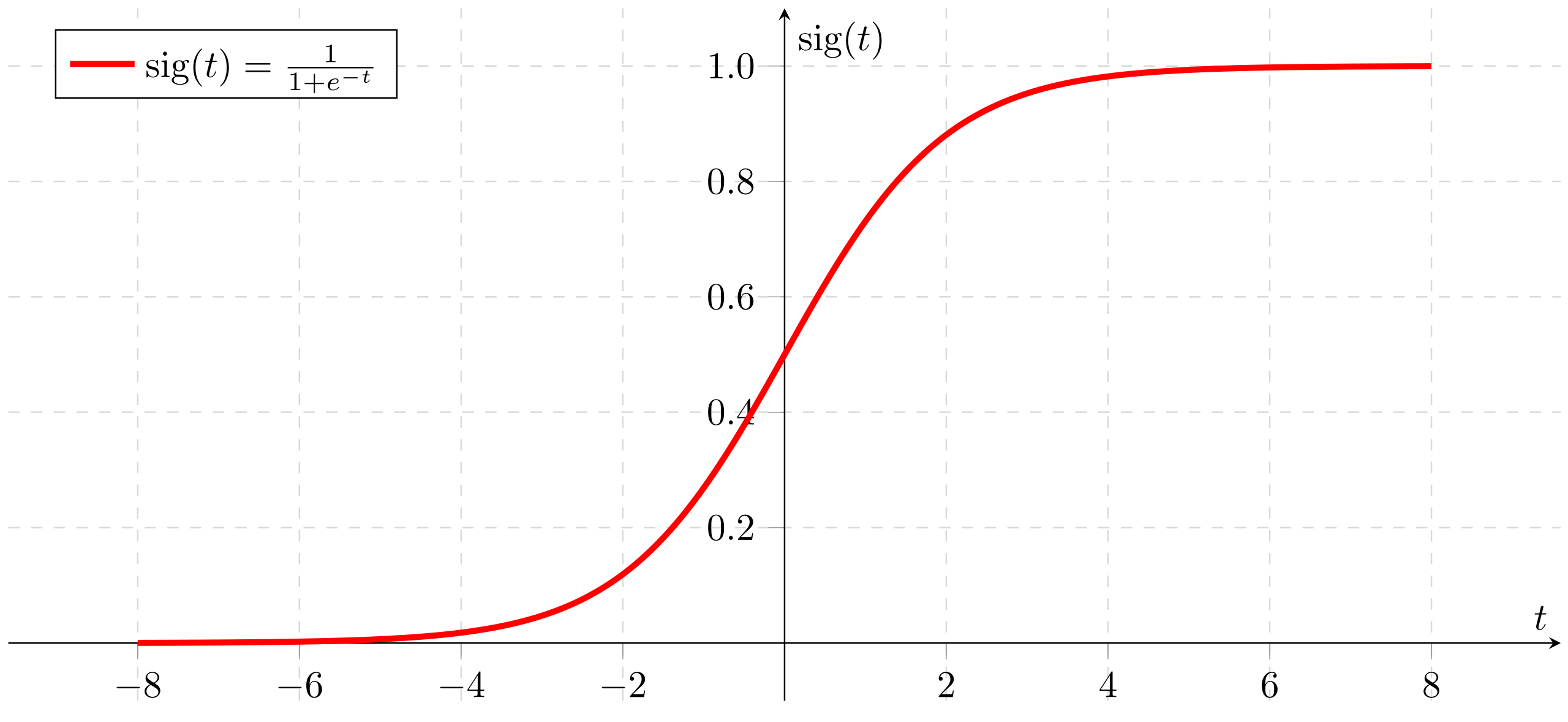
Nell'espressione precedente, notiamo che:

\(y\) è l'uscita della regressione logistica;
\(z\) è pari, per un generico modello lineare, a \(b + w_1 x_1 + \ldots + w_N z_N\).

Funzione di costo¶

La funzione di costo per la funzione logistica è chiamata log loss, ed è espressa come:

\[ LogLoss = \sum_{(x, y) \in D} -y log(y') - (1 - y) log (1 - y') \]

dove:

\((x, y)\) sono le coppie date da feature e label nel dataset \(D\);
\(y\) è la label vera per un dato insieme di feature;
\(y'\) è il valore predetto.

Soglia di decisione¶

La regressione logistica restituisce quindi una probabilità, la quale dovrà essere in qualche modo "convertita" in un valore relativo ad una classe.

Tornando al nostro esempio, un modello che restituisce una probabilità \(p\) pari a \(0.999\) ci dice che, molto probabilmente, il messaggio elaborato è di spam. Di converso, nel caso il modello restituisca una probabilità \(p\) pari a \(0.003\), allora è molto probabile che il messaggio non sia spam. Cosa accade, però, quando \(p\) è pari a \(0.495\)?

Essendo il nostro modello deterministico, è necessario passare da un valore puramente numerico (ovvero, la probabilità) ad una classe che, nel caso specifico, può essere positiva (messaggio di spam, con \(p\) genericamente "alto") o negativa (messaggio non di spam, con \(p\) genericamente "basso"). Di conseguenza, dovremo definire una soglia decisionale, in base alla quale decideremo che i messaggi con probabilità sopra-soglia sono spam, mentre quelli con probabilità sotto-soglia sono legittimi. Di default, questo valore viene impostato a \(\rho=0.5\); tuttavia, potrebbe essere necessario ridefinirlo sulla base dello specifico problema sotto esame. Ne parleremo più approfonditamente nella lezione dedicata alle metriche.