5.2.5 - Variational autoencoder¶
Abbiamo visto come gli autoencoder classici come gli UAE comprimono l'input \(x\) in una rappresentazione compressa \(h\) a partire dal quale è possibile ricostruire \(x\) stesso. Normalmente, la rappresentazione compressa \(h\) è di tipo deterministico, e permette una ricostruzione simile a quella mostrata in figura 1.

Una rappresentazione \(h\) di tipo deterministico permette di ricostruire in maniera adeguata l'input \(x\). Tuttavia, potrebbe essere interessante valutare come si distribuiscano i parametri caratterizzanti \(h\) all'interno dello spazio della rappresentazione latente: in questo modo, potremmo ottenere delle distribuzioni di probabilità da utilizzare per generare dei dati simili ad \(x\). I variational autoencoder (VAE) si occupano proprio di far questo, generando gli attributi latenti in un modo simile a quello mostrato in figura 2:
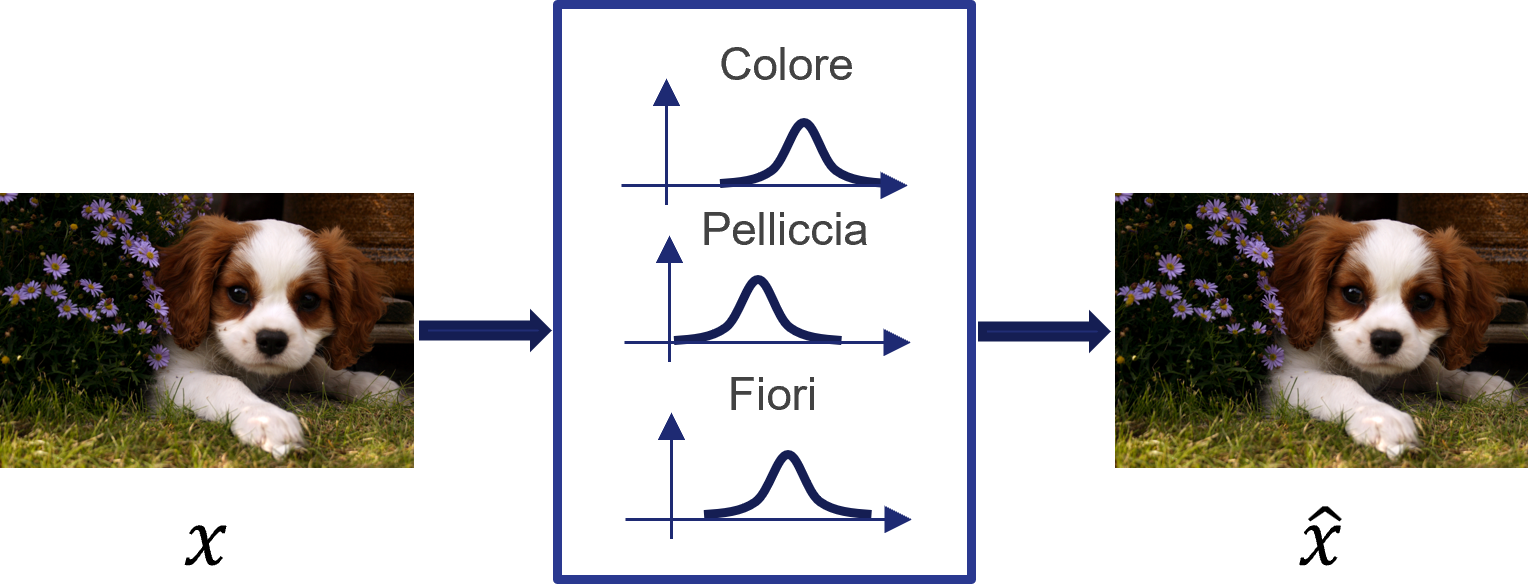
Il motivo per cui gli attributi latenti possono essere espressi sotto forma di distribuzioni di probabilità può essere spiegato come segue. Proviamo ad esempio ad identificare le caratteristiche del vettore latente \(h\) che ricostruisce l'output a partire da un certo input \(x\), modellando la distribuzione \(x[p(z|x)]\).
La stima esatta di questa distribuzione può essere molto costosa dal punto di vista computazionale; in tal senso, un'opzione molto più semplice è costruire un modello parametrizzato \(q\) minimizzando una metrica di distanza, come la divergenza di Kullback-Leibler, tra la distribuzione "vera" e quella parametrizzata. Grazie al modello parametrizzato \(q\) potremo inferire gli attributi latenti ed usarli per ricostruire il dato iniziale. Per quello che riguarda i parametri da utilizzare, questi variano a seconda delle ipotesi fatte su \(h\): infatti, nel caso semplicistico di una distribuzione normale, potremo utilizzare la media e la varianza.
La funzione di costo di un VAE prevede quindi due contributi. Il primo è quello legato alla reconstruction loss che, focalizzandosi soltanto sulla minimizzazione dell'errore di ricostruzione, fa in modo che la rete provi ad apprendere delle distribuzioni estremamente centrate sui parametri che servono a soddisfare questa condizione. L'altro contributo è dato dalla divergenza di Kullback-Leibler, che viene utilizzata per fare in modo che la distribuzione dei parametri sia il quanto più vicina possibile a quella considerata come reale. Di conseguenza, la funzione di costo complessiva può essere espressa come:
dove \(N\) indica la distribuzione normale a media nulla e varianza unitaria, e \(\beta\) è il fattore di peso associato al contributo della divergenza di Kullback-Leibler.